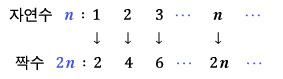
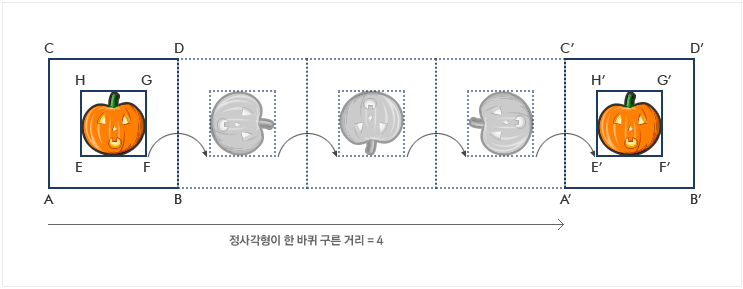
| 역사상 가장 오래 걸린 재판은 무엇일까? 그것은 아마도 갈릴레오에 대한 교황청의 재판일 것이다. 그 내막을 알아보자. 갈릴레오 갈릴레이(Galileo Galilei)는 1564년에 피사(Pisa)에서 플로렌스의 가난한 귀족의 아들로 태어났다. 그는 처음에 의학에 관심이 있었는데 피사 성당의 천장에 매달린 커다란 청동 등불이 진동 폭과 무관한 주기로 앞뒤로 진동한다는 것을 알고 난 후, 관심을 수학으로 돌렸다. 갈릴레오는 25세 때 피사(Pisa) 대학의 수학 교수로 임명되었으며 교수로 재직하는 동안 낙하 물체의 공개 실험을 했다. 이 실험은 무거운 물체가 가벼운 물체보다 빨리 떨어진다고 말한 아리스토텔레스의 이론을 부정하기 위한 것이었다. |
|
|

|
|
|
|
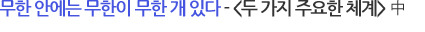
|
|
|

|

[*출처-네이버 백과*]
'게시판3' 카테고리의 다른 글
| 색色있는 서울 (0) | 2009.04.19 |
|---|---|
| 조선시대 희귀자료 모음 (0) | 2009.04.19 |
| 나비 날개의 나노구조 (0) | 2009.04.19 |
| 과일껍질 다양한 활용법 (0) | 2009.04.19 |
| 초대칭 이론 (0) | 2009.04.19 |