운동량 보존법칙-네이버캐스트

물리학에서는 보존되는 양이 적지 않다. 보존이 된다는 말은 대체로 어떤 물리량이 시간에 따라 변하지 않는다는 뜻으로 사용된다. 보존량은 물리학에서 무척 중요하다. 그에 따라 무슨 무슨 보존법칙들도 많이 존재한다.   물리학이란 기본적으로 어떤 물리적 계(system)의 시간에 대한 변화를 살피는 학문이기 때문에, 시간에 따라 변하지 않는 양이 있다면 그 양을 중심으로 물리계를 기술하는 것이 아주 중요한 문제이다. 대표적인 보존량은 지난 회에 살펴보았던 에너지이다.     물체에 가해진 힘은 운동량의 시간에 대한 변화로 표현할 수 있다 에너지 보존법칙만큼이나 물리에서 중요한 보존법칙이 바로 운동량 보존법칙이다. 운동량에는 선운동량(linear momentum)과 각운동량(angular momentum)이 있다.   운동량은 뉴턴이 자신의 역학체계를 세울 때부터 중요한 개념이었다. 지난 가속도의 법칙에서도 잠깐 말했듯이 뉴턴은 운동 상태를 나타내는 물리량으로 운동량을 지목했다.   특히 뉴턴 역학의 핵심이라고 할 수 있는 뉴턴의 제2운동법칙은 아래와 같이 요약할 수 있다.   “법칙2. 운동의 변화는 가해진 힘에 비례하며 힘이 가해진 직선 방향으로 일어난다”

 

여기서 운동의 변화는 운동량의 변화를 의미한다. 이것을 식으로 옮기면 가속도의 법칙에서 보았던 F=ma를 얻는다.   그러나 뉴턴의 언급에 좀 더 가까운 표현을 찾는다면, 힘은 곧 운동량의 시간에 대한 변화이다. 이것을 수식으로 옮기면     라고 쓸 수 있다. 여기서 p가 바로 운동량(혹은 선운동량)이다. 운동량은 물체의 질량과 속도의 곱으로 주어진다(p=mv).  따라서 힘은 (질량이 시간에 대해 변하지 않을 때)     로 F=ma를 쉽게 얻을 수 있다. 여기서 속도(v)의 시간에 대한 변화량(미분)은 가속도(a)임을 이용하였다.

 

그러니까 힘을 운동량의 시간에 대한 변화라고 해도 F=ma를 재현할 수 있다. 뿐만 아니라 운동량의 시간에 대한 변화로 힘을 정의하면 질량이 시간에 따라 변하는 경우(예컨대 로켓의 운동)에도 뉴턴 방정식을 적용할 수 있는 이점이 있다.     외부에서 가해진 힘이 없으면, 운동량은 보존된다 여기서 만약 외부의 힘(F)이 없으면 어떻게 될까? 힘은 곧 운동량의 시간에 대한 변화이니까 힘이 없다는 말은 “운동량의 시간에 대한 변화가 없다”는 말이다. 시간에 대한 변화가 없다! 그러니까 운동량이 곧 보존양이 되는 것이다. 수학적으로도 이는 자명하다.     외력이 없을 때 운동량이 보존된다는 말을 다시 표현하면 처음의 운동량이 나중의 운동량과 항상 같다는 말이 된다. 그런데 운동량은 물체의 질량과 속도의 곱으로 주어진다고 했으니까 운동량 보존법칙을 식으로 표현하면 다음과 같다.     여기서 m은 질량이고 v는 속도이다. 첨자 i는 그 양이 처음 값(initial)을 나타내고 f는 그 양이 나중 값(final)을 나타낸다. 이 식을 보면 로켓이 연료를 내뿜으며 어떻게 추진력을 얻는지 (혹은 작용-반작용이 어떻게 적용되는지) 힌트를 얻을 수 있다.   로켓은 자기 질량의 일부인 연료를 로켓의 진행과 반대방향으로 분사하여 추진력을 얻는다. 로켓은 원래 정지해 (vi=0) 있었지만 연료를 뒤로 내뿜게 되면 연료는 지면 방향으로 운동량을 얻는다. 그러나 원래 연료+로켓의 운동량은 0이었으니까 연료의 운동량을 상쇄하기 위해서 로켓의 본체는 위 방향으로 운동량을 얻는다.

 

운동량이 보존되는 기본원리는 망망한 우주에 내버려진 우주인을 상상해 보면 짐작이 간다. 이 우주인은 아무리 발버둥을 쳐도 자기가 있는 자리에서 꼼짝도 할 수가 없다. 우주공간이 공기나 물로 채워져 있다면 헤엄치듯이 나아갈 수도 있겠지만 우주는 텅 비어 있다. 우주인이 몸을 오른쪽으로 움직이려고 하면 똑같은 몸의 일부는 항상 그 반대쪽으로 향하게 마련이다. 이 우주인이 자기가 원하는 방향으로 움직이려면 그 반대방향으로 뭔가를 내버려야만 한다. 몸에 지닌 장비든 소변 같은 배설물이든 무언가가 반대 방향으로 운동량을 갖고 자기 몸을 떠나가야만 한다.   운동량은 속도나 힘과 마찬가지로 크기와 방향을 가지고 있는 벡터(vector)양이다. 벡터의 가장 큰 특징은 공간에 따라 각 성분이 존재한다는 것이다. 그래서 운동량도 x성분, y성분, z성분이 존재한다.   운동량이 보존될 때는 이 세 가지 모든 성분이 각각 보존된다. 즉, x 방향의 운동량은 y성분이나 z성분과 상관없이 그 자체로 보존되고 y 방향의 운동량이나 z 방향의 운동량도 마찬가지이다. 그래서 운동량이 보존되는 조건은 물리학에서 매우 강력한 조건이다. 에너지 보존법칙에서 이미 소개했듯이 상대성이론에서는 에너지가 운동량의 시간성분으로 들어와서 4차원의 운동량을 형성한다. 따라서 별도의 에너지 보존법칙을 말하지 않더라도 그냥 운동량이 보존된다고 하면 그 시간성분인 에너지도 함께 보존된다고 생각할 수 있다.

 

 

운동량이 보존되는 근본적인 이유는 공간이 ‘균질’하기 때문이다 운동량이 보존되는 근본적인 이유는 우리가 살고 있는 이 공간이 기본적으로 균질(homogeneous)하기 때문이다. 공간이 ‘균질하다’는 뜻은 공간 어디에도 특별히 유별난 곳이 없이 공간의 모든 점이 물리적으로 동등하다는 뜻이다. 공간의 균질성을 좀 더 과학적으로 설명하자면 이렇다. 내가 지금 물리적 계를 A라는 지점에서 관찰한 내용과 A에서 좀 떨어진 임의의 장소 B라는 곳에서 관찰한 내용이 똑같으면 공간은 ‘균질하다’고 말할 수 있다.   문제를 단순화시키기 위해 1차원 공간 속에서의 1차원 운동만 생각해 보자. 지금 어떤 물리계 S가 어떤 운동량 p를 가지고 점 A를 지나가고 있다. 이대로라면 S는 머지않아 A에서 좀 떨어진 B라는 점을 지나갈 것이다. 만약 S에 힘이 가해지지 않는 경우, 점 A와 점 B가 물리적으로 동등하다면 B에 있는 관측자는 얼마 전 A에 있는 관측자가 관찰한 S의 운동 상태, 즉 운동량 p와 똑같은 운동 상태를 보게 될 것이다. 혹은 A의 관측자가 자기도 모르게 갑자기 B의 위치로 옮겨졌다 하더라도 S의 운동에 근본적인 변화가 있다고 느끼지 못할 것이다.   즉 운동량 p는 보존되는 양이다. 만약 점 A와 B가 물리적으로 동등하지 않다면 S의 운동 상태는 A와 B에서 서로 다르게 기술될 것이다. 말하자면 서울에서의 물리 법칙과 브라질리아에서의 물리 법칙이 달라질 것이다.

 

 

 

이것을 좀 더 기술적으로 말하자면, 운동량은 어떤 계의 위치를 이동시키는 것과 관련된 물리량이다. 반면에 에너지는 시간을 돌리는 것과 관련된 물리량이다. 그래서 에너지가 보존되는 이유는 물리계가 시간에 대한 대칭성을 가지고 있기 때문이라고 할 수 있다. 일반적으로 물리계와 관련된 대칭성이 있으면 (물리계 자체가 대칭적일 필요는 없다.) 반드시 그에 상응하는 보존량이 존재한다. 이를 뇌터의 정리(Noether's theorem)라고 부른다. 뇌터(Amalie Emmy Noether, 1882~1935)는 독일 출신의 여성 수학자로서 1918년 이 정리를 발표했다.

 

공간이 균질하다는 성질은 언뜻 생각하기에 무척 당연해 보이지만 적어도 갈릴레이 시절까지는 그렇지 않았다.   천동설에 의하면 지구는 우주의 중심으로서 우주 공간에서 매우 특별한 지위를 점하고 있었다. 그러나 지동설에 의하면 지구는 우주의 평범한 위치를 떠돌아 다닐 뿐이다. 과학과 기술이 발전하면서 인류는 천상의 비밀을 하나씩 벗겨 왔고 이제 우리는 우주의 어느 위치도 다른 여느 위치와 다르지 않다고 매우 확신하게 되었다. 한편 공간은 균질적이기도 하지만 또 매우 등방적이다. 등방적이라는 말은 우리가 한 지점에 서서 어딘가를 바라보는 방향이 달라지더라도 차이가 없다는 말이다. 직관적으로 생각해 봐도 물리법칙은 우리가 어느 방향을 보고 있느냐에 따라 달라지지 않을 것이다. 우리가 동쪽을 바라보고 실험을 하든 북쪽을 보고 실험을 하든 그 결과는 항상 똑같을 것이다. 만약 그렇지 않다면, 그렇게 방향에 따라 달라지는 법칙은 ‘법칙’으로서의 자격이 없다. 물리학자들은 이 경우에 방향에 따라 달라지지 않는 새로운 법칙을 찾으려고 노력할 것이다. 공간이 등방적이라면 뇌터의 정리에 따라 그에 상응하는 보존량이 있어야 한다. 그 양은 각운동량(angular momentum)이라는 양으로서 회전 운동과 관련된 운동량이다. 곧 오늘의 과학을 통해 각운동량에 관한 내용을 다룰 예정이다.

 

 

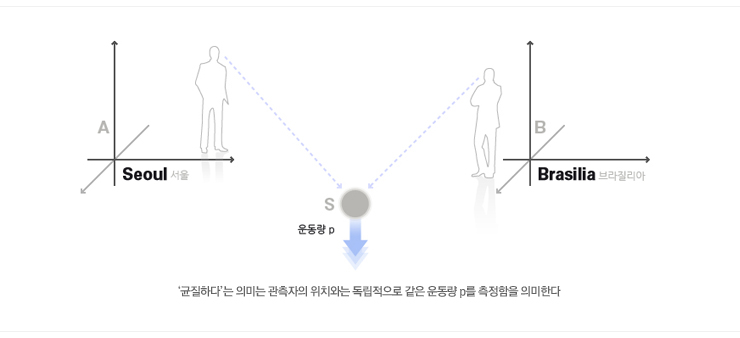
물리 법칙에서 보존되는 양이 중요하듯, 인간 세상에서도 변치 않아 좋은 것이 많다 변하지 않는 양이 물리에서만 좋은 것은 아니다. 사람 사는 세상에서도 변하지 않았으면 하고 바라는 것들이 많다. “변화가 제일 쉬웠다”는 어느 광고 카피도 있듯이 대체로 급변하는 환경에 맞춰 스스로 능수능란하게 변할 수 있는 능력이 각광을 받는 것이 현실이다. 하지만 때로는 변하지 않는 그 무엇이, 그 변하지 않는 가치 때문에 돈이 되기도 한다. 예컨대 다이아몬드는 그 불변성 때문에 변하지 않는 사랑의 징표로 오랫동안 널리 애용되어 왔다. 때가 되면 그리고 종종 불경기 때는, 복고 열풍이 부는 것도 옛 것에 대한 그리움 때문이 아닐까? “옛날 가격 그대로”라는 문구는 금전적으로도 매력적일 뿐만 아니라 변하지 않는 무엇을 갈망하는 사람들의 마음을 사로잡는다. 휴대전화를 바꿀 때도 전화번호가 그대로 바뀌지 않았으면 하는 바람은 누구나 가지고 있다.   이름난 음식점을 갈 때마다 우리는 항상 그 집의 맛이 언제나 똑같을 것이라는 기대를 안고 간다. 맛이 바뀌면 단골들은 옛 맛을 그리워하며 발길을 돌린다. “장맛이 바뀌면 운암정 문을 닫아야 한다”는 <식객>의 원리는 그래서 예사롭지 않다. 맛뿐만 아니라 음식을 먹는 공간 자체도 사람들 뇌리에는 깊이 박혀 있다. 같은 음식이라도 장소에 따라 그 맛이 다르게 느껴지기도 한다. 그래서 무턱대고 크게 신장 개업했다가 다시 문 닫는 음식점을 우리는 심심찮게 볼 수 있다. 대한민국은 매우 짧은 시간 동안에 역사상 유래를 찾기 어려울 정도로 많은 성과를 이루었다. 그러다 보니 우리 주변에는 미처 챙기지 못한, 변하지 않는 가치들도 적지 않다. 이제 거의 다 철거되고 사라진 종로의 피맛골도 그 중의 하나일 것이다. 그나마 요즘 우리의 옛 것, 변하지 않는 것의 가치에 대한 관심이 점차 높아지고 있어 다행스럽다.

 

 

 

글 이종필 / 고등과학원 물리학부 연구원

 

서울대학교 물리학과를 졸업하고 동 대학에서 입자물리이론으로 박사학위를 받았다.

현재 고등과학원 물리학부의 연구원이다.

저서로는 <신의 입자를 찾아서>, <대통령을 위한 과학 에세이>가 있고,

역서로는 <최종이론의 꿈>이 있다.

 

이미지 TOPIC / corbis